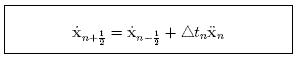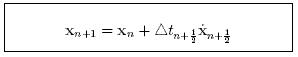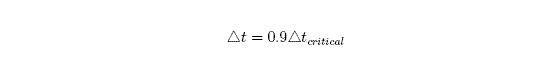Equation of Motion
Single degree of freedom system
Forces acting on mass m
Equilibrium – d Alembert s principle : 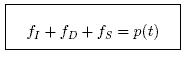
Equation of motion for linear elasticity :
 linear ordinary d.e.
linear ordinary d.e.
Nonlinear case :
 nonlinear ordinary d.e.
nonlinear ordinary d.e.
Analytical solutions of linear ordinary di erential equations are available.
Dynamic response of linear undamped system due to harmonic loading:
Direct Integration of Equation of Motion
- For nonlinear problems only numerical solutions are possible.
- Focus is on explicit methods, in particular Central Difference method.
- LS-DYNA uses a modification of the central di erence time integration.
- Central difference scheme is an explicit method.
- For explicit schemes the equation of motion is evaluated at the old time step tn, whereas implicit methods use the equation of motion at the new time step tn+1.
Central Difference
Substitute equations (??) and (??) into (??) :
- For lumped mass and damping the matrices M are diagonal.
- Inversion of diagonal matrices M and C is trivial.
- At timer t = 0 we have initial conditions u0 and &u-odot0. From equilibrium we find ü0. From equation (??) and (??) :
- The central di erence scheme is conditionally stable, i.e. the size of the time step is limited.
Stability of the Central Difference Scheme
Uncouple the system of linear equations of motion into the modal equations.
Φ … modal matrix with M-orthonormalized eigenvectors stored in columns N uncoupled equations of motion with generalized displacements χ :
central differences :
Substitute xn and xn into equation of motion () at time t^n* :
In matrix form
A… time integration operator for discrete
For m-time steps and L = 0
Spectral decomposition of A :
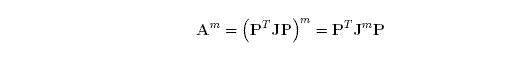
P … orthonormal matrix; contains eigenvectors of A
J … Jordan form; eigenvalues λi of A are stored on diagonal
spectral radius = ρ(A) = largest eigenvalue of A = max ((diag(J))
Eigenvalues of A for the undamped equation of motion
For the damped equation of motion :
Damping reduces the critical time step.
For varying time step sizes :
- The time integration is stable, if the time step size decreases.
- The time step is bounded by the largest natural frequency of the structure.
- For shells: bending and membrane modes are present the frequency of the membrane mode usually limits the critical time step, since membrane stiffness is much larger than bending stiffness
Critical time step of a rog
Time Integration in LS-DYNA
- discretization In LS-DYNA actual geometry x is used instead of displacements. Thus x replaces u.
- difference formula :
equation of motion at time t^n for the nonlinear case:
(asynchronous damping)
assumption :
 update of accelerations
update of accelerations
update formulas for velocities and displacements:
From (2):
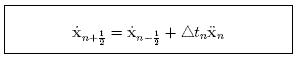
From (1):
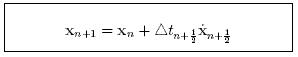
Remarks :
- starting procedure for first time step with
- Standard central di erence method approximates time step limit for LS-DYNA time integration scheme.
- No stability proofs are available for time integration of nonlinear problems. Default in LS-DYNA :
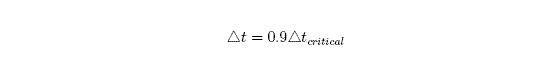
- critical time step for varying time increments


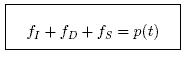

 linear ordinary d.e.
linear ordinary d.e. nonlinear ordinary d.e.
nonlinear ordinary d.e.













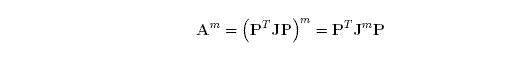






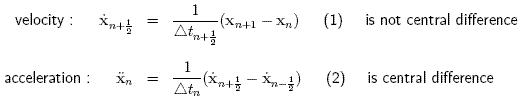


 update of accelerations
update of accelerations