Crashworthiness Optimization

Problem Description

 The problem is of a simplified vehicle moving at a constant velocity and crashing into a pole.

 vehicle_crash1.png vehicle_des_var2.png
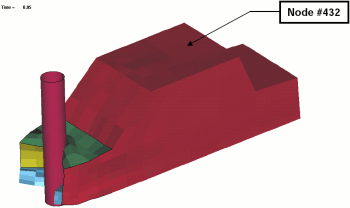
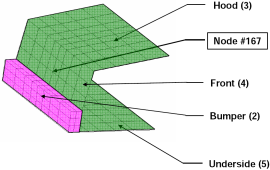
Fig. 1(a): Deformed vehicle after 50 ms Fig. 1(b): Design variables with part numbers

The problem illustrates the following features:

  • A simple single iteration optimization
  • Dealing with an infeasible design formulation
  • Use of composite functions
  • Trade-off study
  • Use of the LS-DYNA result interface
  • Discrete-continuous optimization

The criteria of interest are the following:

  • Head injury coefficient (HIC) of a selected point (15ms)
  • Component Mass of the structural components (bumper, front, hood and underside)
  • Intrusion computed using the relative motion of two points

Design variables:

  • The hood, front and underside (parts 3, 4 and 5 in Fig. 1(b)) are grouped under a single design variable: thood
  • The bumper (part 2 in Fig. 1(b)) is identified as another design variable: tbumper

Design Formulation

The design formulation is as follows:

  • Minimize HIC(15 ms) subject to Intrusion (50 ms) < 550 mm. The intrusion is measured as the distance between the nodes 167 and 432 (for the location of the nodes see Fig. 1).

Possible Approaches for Problem Solution

Downloads

Conclusion

  • The opimization problem has been summarized with the following conclusion:

Conclusion to Crashworthiness Optimization

 

  • The solution of the optimization problem presented in the example for detemining the optimal thickness of the bumper and the hood has been obtained with the three methodologies viz. Single Stage, SRSM continuous and Discrete method.
  • The choice of the optimum design parameters ( tbumper, thood ) is based on the objective of reducing the Head Injury Criteria (HIC).
  • The given constraint for the optimization problem is the permissible intrusion, measured as the distance between the nodes 167 and 432.
  • A discrete variable has been incoporated to illustrate a more practical approach for structural optimization due to the limitations in manufacturing processes.
  • A tabulated comparision of the results obtained by the three approaches has been produced below.
Single Stage Continuous (SRSM) Discrete (SRSM)
 thood 1.54 1.56 2
 tbumper 5 5 5
 HIC 37.4 126.3 173.4
 Mass 0.656 0.659 0.7597
 Intrusion 550 550 539
 RMS Error (HIC) 27.7% 3.43% 4.61%
 SPRESS (HIC) 91.4% 11% 13.7%
 R-sq (HIC) 0.922 0.837 0.994
 Table: Comparision of results with three methods of optimization

Results

 

  • The discrete method presented using the SRSM metamodel presents comparable results to the SRSM continuous variables.
  • The RMS error using the Single Stage yields relatively higher values, but the computation cost is less. Hence it is useful for a raw estimate of various parameter studies in the initial execution.
  • The SPRESS value of the SRSM presents better validation compared to the Single Stage method. Hence the prediction for the SRSM method builds more confidence in the metamodel.
  • Note that for the sequential approaches, the metamodel only represents the subregion of the design space of the respective iteration, it’s not a global approximation.